How Particle Swarm Optimization Works: A Step-by-Step Guide?

Particle swarm optimization (PSO) is a popular optimization method that is based on how birds and fish interact with each other.

Inspired by animal social behaviour, including that of birds and fish, particle swarm optimization (PSO) is a method of optimization. This approach searches for the best answer to a problem using a set of particles, reflecting various solutions. Because of its simplicity and efficiency, this technique is frequently applied in disciplines including engineering, data science, and machine learning.

This guide will cover PSO’s essential ideas, parameters, and pragmatic uses. The intention is to simplify the PSO idea and demonstrate how to apply it to address optimization challenges.

What Is Particle Swarm Optimization?

PSO is a method inspired by collective animal movements in search of food. Imagine a swarm of birds hunting in a field. Every bird—or particle—searching the field looks for the ideal place. Searching, they provide details on excellent locations, guiding the group towards the finest potential venue.

Every particle in PSO stands for a possible fix for the issue. Searching for the optimum solution, the particles travel inside a specific area known as the search space. Their own experience, as well as the experiences of other group members, direct their movement.

Particle Swarm Optimization Not Like Other Approaches of Optimisation

PSO employs several particles instead of Gradient Descent, which finds the optimal solution from one point. This enhances the possibility of discovering the best solution and enables PSO to investigate more of the search area. Gradient Descent finds the optimal direction using the derivative of a function, so there is no need for gradient knowledge. Conversely, PSO does not require this data. For problems where the function isn’t smooth or differentiable, PSO helps because of this. Every particle in PSO tracks the global best solution—that which any particle has discovered—and its personal best solution—that it has thus far found. This lets particles be directed over time towards improved solutions.

Essential PSO parameters and their effects

Several factors affect PSO’s performance; each one affects particle motion and exploration of the search space:

• More particles mean a higher opportunity to investigate several solutions. Still, a lot of particles also lengthen computing times.
• Equations considering the particle’s present position, personal best, and global best position help to define the speed at which particles migrate. This enables particles to change their motion in response to learning.
• This controls the current movement of a particle by its past velocity. A smaller weight concentrates on local search; a bigger inertia weight means the particles explore a greater area.
• Whereas the social factor follows the worldwide best solution of the swarm, the cognitive factor makes a particle depend on its best answer. Particle maintenance of both uniqueness and social learning depends on juggling both elements.
• Topology is the study of particle interactions. An ultimately linked topology, for instance, implies that every particle shares information with all others, whereas a ring topology limits communication to adjacent particles.

Particle Movement in PSO

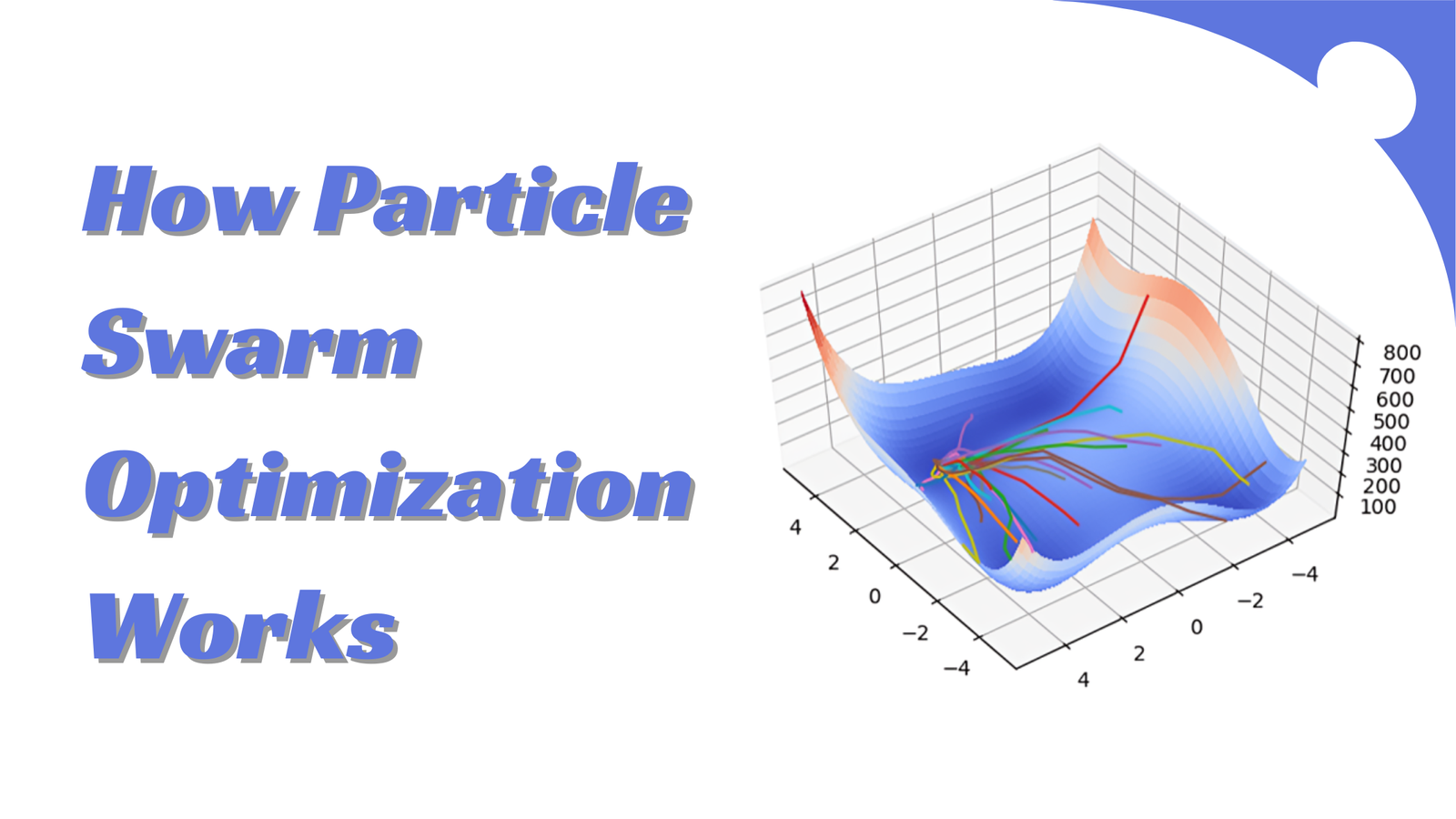
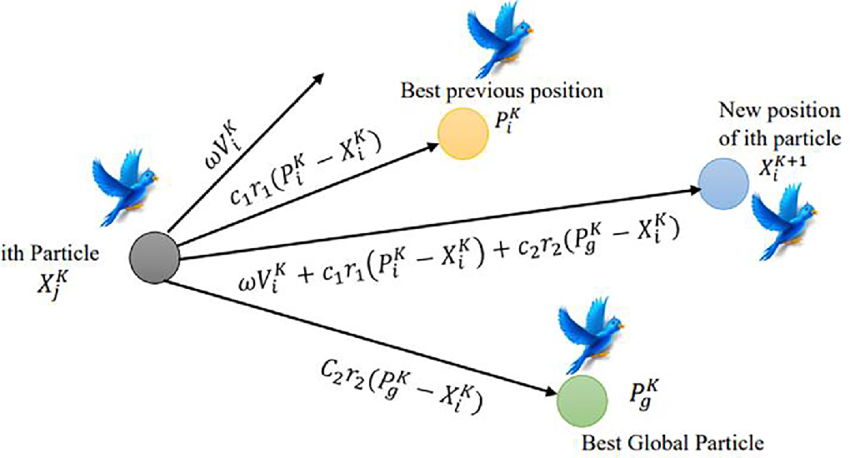
Every particle in PSO moves in response to its velocity, computed using a formula comprising its personal best position, the global best position, and a random element. It looks like this:

• The velocity formula considers the particle’s past speed, relative proximity to its personal best, and global best solution proximity. Variability in every iteration is introduced via random numbers, avoiding particle stagnation.
• Once the velocity is computed, adding it to the existing position finds the new position. This lets the particle cross the search area in the most favourable direction.
• These processes continue until the particles gather on the ideal solution or until the maximum number of iterations is attained.

The Global Best Solution Discovery

Comparing the solutions of all the particles helps one identify the global best solution in PSO by choosing the best performance. A fitness function evaluates the quality of every solution, using which one can ascertain their relative goodness for the current challenge. The fitness function assigns a score depending on how near the optimal outcome each particle’s position is assessed. Should a particle discover a better solution than the present global best, that solution takes the front stage. This revised data guides other particles toward improved solutions.

Solving Various Kinds of Problems with PSO

These deal with determining ideal values for variables capable of any actual number. PSO can gently change the particle placements in the ongoing search area. Discrete problems are those with particular, unique values for solutions. Although PSO was first intended for continuous environments, it can be modified for discrete situations using tailored movement rules for particles.

PSO Algorithm Convergent Behaviour

Reducing the inertia weight as the iterations go helps direct the attention from worldwide exploration to local exploitation, boosting convergence. Typical termination criteria are achieving maximum iterations or halting when improvements fall below a particular level. Convergence guarantees the particles finally zero in on the best solution and is not ceaselessly exploring.

Combining Other Methods with PSO

• Combining particle swarm optimization with other optimization techniques will help maximize performance.
• PSO can be used with local search techniques, which concentrate on fine-tuning the solution once a promising area has been discovered.
• Together with PSO, simulated annealing can help the algorithm explore new areas and escape local optima.
• These combinations provide PSO additional strength in addressing challenging optimization challenges.

The function of initial positions in PSO

The starting placements of particles can significantly influence the result of PSO.

• Starting from random points lets the particles investigate several sections of the search space.
• Targeted Initialisation: Faster convergence can result from targeted initialization should some information about the solution be known.
• Selecting the correct initialization technique guarantees a comprehensive search for the best solution by helping to balance exploration and exploitation.

PSO’s Problems and Restraints

Particle Swarm Optimization has specific difficulties, even if it is mighty:

• Sometimes, PSO concentrates too extensively on local solutions, particularly in cases with a complicated search area.
• More significant numbers of particles and iterations might speed up the search for a solution in computational terms.
• Changing variables like inertia, weight, and learning factors require experience and tailored changes based on the problem.
• Despite these difficulties, PSO is still a popular tool since it can be readily modified and used for different issues.

Ultimately

Why PSO’s popularity is such An easy-to-use and robust approach for optimizing issues is particle swarm optimization. Its accessibility for numerous uses stems from its capacity to investigate a large search space free from complicated mathematical computations. PSO offers a versatile and potent method for identifying ideal solutions, whether your project is an engineering design or a machine learning one. Understanding its fundamental ideas and constraints will help you apply PSO to address different optimization difficulties.